在一些统计或者排序的算法中,常常要用到样本方差这个东西,来判断一组数据的离散程度。
这是样本方差的公式:
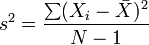
49_3710_b4f761117e4bb21.png[删除]
然而,在计算机编程中,往往需要计算运行方差(running variance),因为样本的个数总是的在不断变化的,确切将是不断递增;如果每次增加,都要重新计算平均值,再按次公式,计算出方差;虽可以实现,但计算量会随着数据的增长变的太大。
因此,递推的公式就显得格外重要;通过n-1个样本时的方差值,和新增的样本,就能得到此时这N个样本的方差;这样计算量不会变同时保持在一个很小的值,可大大提高程序的计算效率。递推公式如下:
Mn = Mn-1+ (xn - Mn-1)/n
Sn = Sn-1 + (xn - Mn-1)*(xn - Mn)
Mn为平均值,初始时: M1 = x1, S1 = 0 (此等式的推导证明,我后面给出),而样本方差 s =Sn/(n - 1)
下面是我自己给出的简单实现(若有更好的实现,请不吝赐教)
01 package com.mycode.math;
02
03 public final class RunningVariance {
04 private int count;// 样本的个数
05 private double mk;// 平均值
06 private double sk;// Sn
07 private double runVar;// 样本方差
08
09 public RunningVariance() {
10 this(0, 0.0, 0.0);
11 }
12
13 public RunningVariance(int count, double mk, double sk) {
14 this.count = count;
15 this.mk = mk;
16 this.sk = sk;
17 recomputeRunVar();
18 }
19
20 public double getMk() {
21 return mk;
22 }
23
24 public double getSk() {
25 return sk;
26 }
27
28 /**
29 * 获取运行时样本方差
30 *
31 * @return
32 */
33 public synchronized double getRunningVariance() {
34 return runVar;
35 }
36
37 /**
38 * 增加样本
39 *
40 * @param sample
41 */
42 public synchronized void addSample(double sample) {
43 if (++count == 1) {
44 mk = sample;
45 sk = 0.0;
46 } else {
47 double oldmk = mk;
48 double diff = sample - oldmk;
49 mk += diff / count;
50 sk += diff * (sample - mk);
51 }
52 recomputeRunVar();
53 }
54
55 /**
56 * 移除样本
57 *
58 * @param sample
59 */
60 public synchronized void removeSample(double sample) {
61 int oldCount = getCount();
62 double oldmk = mk;
63 if (oldCount == 0) {
64 throw new IllegalStateException();
65 }
66 if (--count == 0) {
67 mk = Double.NaN;
68 sk = Double.NaN;
69 } else {
70 mk = (oldCount * oldmk - sample) / (oldCount - 1);
71 sk -= (sample - mk) * (sample - oldmk);
72 }
73 recomputeRunVar();
74 }
75
76 private synchronized void recomputeRunVar() {
77 int count = getCount();
78 runVar = count > 1 ? sk / (count - 1) : Double.NaN;
79 // 若需要计算标准差
80 // runVar = count > 1 ? Math.sqrt(sk / (count - 1)) : Double.NaN;
81 }
82
83 public synchronized int getCount() {
84 return count;
85 }
86 }
对于递推公式 Sn = Sn-1 + (xn - Mn-1)*(xn - Mn),我自己做了个简单的推导证明,如下图:
另:图中所提的 等式1 即是 平均数的递推公式:Mn = Mn-1+ (xn - Mn-1)/n

49_3710_9e3e4d24f416581.jpg[删除]